
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:40.
- Naposledy zmenené 2025-06-01 05:06.
Fermatova malá veta uvádza, že ak p je prvočíslo, potom pre každé celé číslo a je číslo a p - a je celočíselný násobok p. ap ≡ a (mod p). Špeciálny prípad: Ak a nie je deliteľné p, Fermatova malá veta je ekvivalentné tvrdeniu, že a p-1-1 je celočíselný násobok p.
Ako týmto spôsobom dokážete Fermatovu malú vetu?
Nech p je prvočíslo a ľubovoľné celé číslo, potom ap = a (mod p). Dôkaz. Výsledok je trival (obe strany sú nula), ak p delí a. Ak p nedelí a, potom stačí vynásobiť kongruenciu v Fermatova malá veta by a dokončiť dôkaz.
Tiež viete, aké je riešenie Fermatovej poslednej vety? Riešenie pre Fermatova posledná veta . Fermatova posledná veta (FLT), (1637), uvádza, že ak n je celé číslo väčšie ako 2, potom nie je možné nájsť tri prirodzené čísla x, y a z, kde je splnená rovnosť (x, y) > 0 v xn+yn =zn.
Vzhľadom na to, prečo je dôležitá Fermatova malá veta?
Fermatova malá veta je základom teorém v elementárnej teórii čísel, ktorá pomáha vypočítať mocniny celých čísel modulo prvočísla. Je to Eulerov špeciálny prípad teorém , a je dôležité v aplikáciách elementárnej teórie čísel, vrátane testovania primality a kryptografie s verejným kľúčom.
Čo znamená Eulerova veta?
Eulerova veta . Zovšeobecnenie Fermata teorém je známy ako Eulerova veta . Všeobecne, Eulerova veta uvádza, že „ak p a q sú relatívne prvočísla, potom “, kde φ je Eulerov funkcia totient pre celé čísla. To znamená, že je to počet nezáporných čísel, ktoré sú menšie ako q a relatívne prvočíslo k q.
Odporúča:
Ako urobíte Punnettov štvorec?
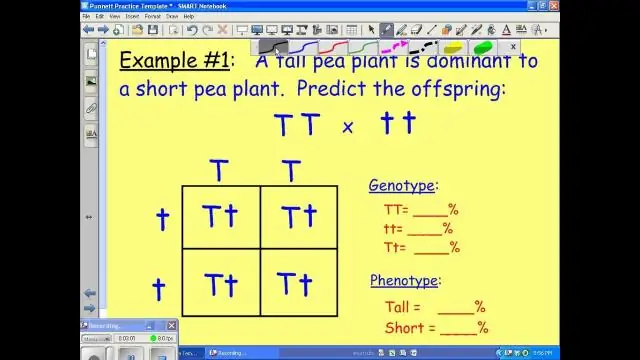
Kroky Nakreslite štvorec 2 x 2. Pomenujte príslušné alely. Skontrolujte genotypy rodičov. Označte riadky genotypom jedného rodiča. Označte stĺpce genotypom druhého rodiča. Nechajte každé políčko zdediť písmená zo svojho riadka a stĺpca. Interpretujte Punnettov štvorec. Opíšte fenotyp
Ako urobíte farbenie karbol Fuchsin?
Návod na prípravu 1% Carbol fuchsinu: Pomocou digitálnych váh odvážte 1 g Basic fuchsinu do sterilnej 100 ml banky. 2. Pridajte 100 ml absolútneho alkoholu a farbivo rozpustite umiestnením do vodného kúpeľa s teplotou 60° C. Vyhnite sa priamemu ohrevu (Riešenie 1)
Ako urobíte najlepšiu sopečnú erupciu?

Sopka bikarbóna a ocot Plastový pohár (vyskúšali sme fľašu s vodou, ale plastový pohár fungoval oveľa lepšie) Voda. Minimálne 3-4 PL sódy bikarbóny (zvyčajne robíme 4-6, vďaka čomu bude extra penivý a urobí 2-3 erupcie) 1 ČL saponátu. 1/2 oz až 2 oz umývateľnej farby, v závislosti od intenzity požadovanej farby
Ako urobíte Punnettov štvorec s viacerými alelami?
Je dôležité, aby ste dodržali potrebné kroky! Najprv musíte založiť svoj rodičovský kríž, alebo P1. Ďalej musíte urobiť 16 štvorcových Punnettov štvorec pre vaše 2 vlastnosti, ktoré chcete prekrížiť. Ďalším krokom je určiť genotypy dvoch rodičov a priradiť im písmená reprezentujúce alely
Ako zistíte vetu o strednom segmente trojuholníka?

Veta o strednom segmente trojuholníka hovorí, že úsečka spájajúca stredy ľubovoľných dvoch strán trojuholníka bude spĺňať nasledujúce vlastnosti: Úsečka bude rovnobežná s treťou stranou. Dĺžka úsečky bude jedna polovica dĺžky tretej strany
