Obsah:
Video: Ako vyriešite lineárnu rovnicu pomocou Gaussovej eliminácie?
2024 Autor: Miles Stephen | [email protected]. Naposledy zmenené: 2023-12-15 23:40
Ako používať Gaussovu elimináciu na riešenie sústav rovníc
- Môžete vynásobiť ľubovoľný riadok podľa konštanta (iná ako nula). násobí riadok tri podľa –2, čím získate nový rad tri.
- Môžete prepínať ľubovoľné dva riadky. vymení riadky jeden a dva.
- Môžete pridať dva riadky dohromady. pridá riadky jeden a dva a zapíše to v rad dva.
Ako potom funguje Gaussova eliminácia?
voľne povedané, Gaussova eliminácia funguje zhora nadol, aby sa vytvorila matrica vo forme echelónu, zatiaľ čo Gauss -Jordánsko eliminácia pokračuje kde Gaussovský prestaneme pracovať zdola nahor, aby sme vytvorili matricu v redukovanej forme. Technika bude ilustrovaná v nasledujúcom príklade.
Okrem toho, čo sú matice Cramerových pravidiel? Cramerovo pravidlo pre systém 2×2 (s dvoma premennými) Cramerovo pravidlo je ďalšou metódou, ktorá dokáže riešiť sústavy lineárnych rovníc pomocou determinantov. Pokiaľ ide o zápisy, a matice je pole čísel uzavretých v hranatých zátvorkách while determinant je pole čísel ohraničených dvoma zvislými čiarami.
Po druhé, aký je účel Gaussovej eliminácie?
Gaussova eliminácia . Z Wikipédie, voľnej encyklopédie. Gaussova eliminácia , tiež známy ako redukcia riadkov, je algoritmus v lineárnej algebre na riešenie systému lineárnych rovníc. Obvykle sa chápe ako postupnosť operácií vykonaných na zodpovedajúcej matici koeficientov.
Aký je rozdiel medzi Gaussovou a Gauss Jordanovou elimináciou?
3 odpovede. Gaussova eliminácia pomáha umiestniť maticu vo forme riadkov, zatiaľ čo Gauss - Eliminácia Jordánska vloží maticu do redukovaného riadkového tvaru. Pre malé systémy (alebo ručne) je zvyčajne pohodlnejšie použitie Gauss - eliminácia Jordana a explicitne riešiť pre každú reprezentovanú premennú v maticový systém.
Odporúča:
Ako vyriešite kvadratickú rovnicu pomocou zákona o nulovom faktore?
Z toho môžeme vyvodiť, že: Ak je súčin akýchkoľvek dvoch čísel nula, potom jedno alebo obe čísla sú nula. To znamená, že ak ab = 0, potom a = 0 alebo b = 0 (čo zahŕňa možnosť, že a = b = 0). Toto sa nazýva zákon nulového faktora; a často ho používame na riešenie kvadratických rovníc
Ako algebraicky vyriešite rovnicu absolútnej hodnoty?
RIEŠENIE ROVNÍC OBSAHUJÚCICH ABSOLÚTNE HODNOTY Krok 1: Izolujte výraz absolútnej hodnoty. Krok 2: Nastavte množstvo v zápise absolútnej hodnoty rovnú + a - množstvu na druhej strane rovnice. Krok 3: Vyriešte neznámu v oboch rovniciach. Krok 4: Analyticky alebo graficky skontrolujte svoju odpoveď
Ako vyriešite rovnicu lineárnej nerovnosti?
Existujú tri kroky: Usporiadajte rovnicu tak, aby 'y' bolo vľavo a všetko ostatné vpravo. Nakreslite čiaru „y=“(urobte z nej plnú čiaru pre y≤ alebo y≥ a prerušovanú čiaru pre y) Odtieňujte nad čiaru pre „väčšiu ako“(y> alebo y≥) alebo pod čiaru pre „menej než“(y< alebo y≤)
Ako vyriešite rovnicu izoláciou premennej?
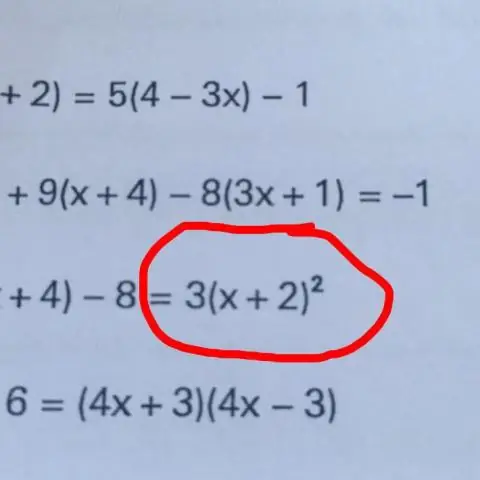
Základnou technikou na izoláciu premennej je „urobiť niečo pre obe strany“rovnice, napríklad sčítať, odčítať, násobiť alebo deliť obe strany rovnice rovnakým číslom. Opakovaním tohto procesu môžeme dostať premennú izolovanú na jednej strane rovnice
Ako vyriešite rovnicu alebo nerovnicu?
Na vyriešenie nerovnice použite nasledujúce kroky: Krok 1 Odstráňte zlomky vynásobením všetkých členov najmenším spoločným menovateľom všetkých zlomkov. Krok 2 Zjednodušte kombináciou podobných výrazov na každej strane nerovnosti. Krok 3 Pridajte alebo odčítajte množstvá, aby ste získali neznáme na jednej strane a čísla na druhej strane